Loans¶
This chapter explains how to manage your loans with GnuCash.
Basic Concepts¶
A loan is defined as a financial transaction in which someone pays for the use of someone else’s money. There are many familiar examples of loans: credits cards, auto loans, house mortgages, or a business loan.
Terminology¶
Before discussing tracking loan in GnuCash specifically, it will be helpful to present a glossary of terminology. The terms presented below represent some of the basic concepts found concerning loans. It is a good idea to become familiar with these terms, or at least, refer back to this list if you encounter an unfamiliar word in the later sections.
Amortization - the repayment plan which will insure that a loan is eventually paid off, typically utilizing equal valued monthly payments. These payments are usually split into principal and interest, where the amount of principal per payment increases (and interest decreases) as the amortization period elapses.
Borrower - the person or company that receives the money from a loan.
Default - when a borrower fails to repay a loan according to the terms agreed upon with the lender.
Deferment - a temporary delay in the repayment of a loan.
Delinquency - is the term that refers to late payments.
Disbursement - amount of the loan paid to the borrower. Some loans have multiple disbursements, meaning the borrower does not receive the full amount of the loan at one time.
Interest - the expense charged by the lender to the borrower for the use of the money loaned. This is typically expressed in terms of a yearly percentage charged on the principal borrowed, known as the Annual Percentage Rate or APR.
Lender - the company or person who lends money to a borrower.
Loan Fee - a processing fee removed from the principal at the time the borrower receives a loan.
Principal - the original amount of the loan, or the amount of the original loan that is still owed. When you make a monthly payment on a loan, part of the money pays the interest, and part pays the principal.
Promissory Note - the legal agreement between the borrower and lender concerning the loan.
Setting Up Accounts¶
When a borrower obtains a loan, it is usually with the intention to make a purchase of something of value. In fact, most loans require the borrower to buy some predetermined asset, such as a house. This asset is insurance against the borrower defaulting on the loan. There are, of course, examples of loans which do not necessarily have an associated high value asset, such as educational loans.
For the account structure presented here, we will assume the loan was used to purchase a compensating asset.
A loan is a liability, the interest you accrue on the loan is an on-going expense, and any administrative fees you may have to pay would be another expense. The thing purchased with the money from a loan is an asset. With these parameters, we can now present a basic loan account structure:
Basic Loan Account Structure
-Asset
-Current Assets
-Savings Account
-Fixed Assets
-Asset Purchased
-Liability
-Loans
-Mortgage Loan
-Expenses
-Interest
-Mortgage Interest
-Mortgage Adm Fees
GnuCash has a number of predefined loan account hierarchies available, including Car Loans and Home Mortgage Loans. To access these predefined account structures, click on Actions > New Account Hierarchy… and select the loan types in which you are interested.
Calculations¶
Determining loan amortization schedules, periodic payment amounts, total payment value, or interest rates can be somewhat complex. To help facilitate these kinds of calculations, GnuCash has a built-in Loan Repayment Calculator. To access the calculator, go to Tools > Loan Repayment Calculator.
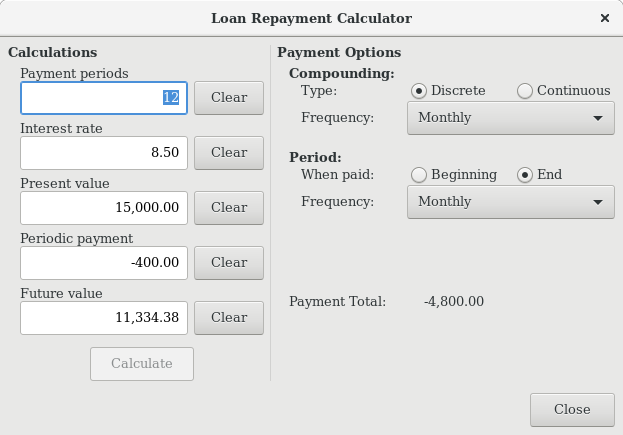
The Loan Repayment Calculator can be used to calculate any one of the parameters: Payment Periods, Interest Rate, Present Value, Periodic Payment, or Future Value given that the other 4 have been defined. You will also need to specify the compounding and payment methods.
Payment Periods - the number of payment periods.
Interest Rate - the nominal interest rate of the loan, ie: the yearly interest rate.
Present Value - the present value of the loan, ie: current amount owed on the loan.
Periodic Payment - the amount to pay per period.
Future Value - the future value of the loan, ie: the amount owed after all payment periods are over.
Compounding - two interest compounding methods exist, discrete or continuous. For discrete compounding select the compounding frequency from the popup menu with a range from yearly to daily.
Payments - the popup menu allows you to select the payment frequency with a range from yearly to daily. You can also select whether your payments occur at the beginning or end of the period. Payments made at the beginning of the payment period have interest applied to the payment as well as any previous money paid or money still owed.
Example: Monthly Payments¶
What is your monthly payment on a $100000 30 year loan at a fixed rate of 4% compounded monthly?
This scenario is shown in the example image above. To perform this calculation, set Payment Periods to 360 (12 months x 30 years), Interest Rate to 4, Present Value to 100000, leave Periodic Payment empty and set Future Value to 0 (you do not want to owe anything at the end of the loan). Compounding is Monthly, Payments are Monthly, assume End of Period Payments, and Discrete Compounding. Now, click on the Calculate button next to the Periodic Payment area. You should see $-477.42.
Answer: You must make monthly payments of 477.42.
Example: Length of Loan¶
How long will you be paying back a $20000 loan at 10% fixed rate interest compounded monthly if you pay $500 per month?
To perform this calculation, leave Payment Periods empty, set Interest Rate to 10, Present Value to 20000, Periodic Payment is -500, and Future Value is 0 (you do not want to owe anything at the end of the loan). Compounding is Monthly, Payments are Monthly, assume End of Period payments, and Discrete Compounding. Now, click on the Calculate. You should see 49 in the Payment Periods field.
Answer: You will pay off the loan in 4 years and 1 month (49 months).
Advanced: Calculation Details¶
In order to discuss the mathematical formulas used by the Loan Repayment Calculator, we first must define some variables. n == number of payment periods %i == nominal interest rate, NAR, charged PV == Present Value PMT == Periodic Payment FV == Future Value CF == Compounding Frequency per year PF == Payment Frequency per year Normal values for CF and PF are: 1 == annual 2 == semi-annual 3 == tri-annual 4 == quaterly 6 == bi-monthly 12 == monthly 24 == semi-monthly 26 == bi-weekly 52 == weekly 360 == daily 365 == daily
Converting between nominal and effective interest rate¶
When a solution for n, PV, PMT or FV is required, the nominal interest rate (i) must first be converted to the effective interest rate per payment period (ieff). This rate, ieff, is then used to compute the selected variable. When a solution for i is required, the computation produces the effective interest rate (ieff). Thus, we need functions which convert from i to ieff, and from ieff to i.
To convert from i to ieff, the following expressions are used:
Discrete Interest: ieff = (1 + i/CF)^(CF/PF) - 1
Continuous Interest: ieff = e^(i/PF) - 1 = exp(i/PF) - 1
To convert from ieff to i, the following expressions are used:
Discrete Interst: i = CF*[(1+ieff)^(PF/CF) - 1]
Continuous Interest: i = ln[(1+ieff)^PF]
Note
In the equations below for the financial transaction, all interest rates are the effective interest rate, “ieff”. For the sake of brevity, the symbol will be shortened to just “i”.
The basic financial equation¶
One equation fundamentally links all the 5 variables. This is known as the fundamental financial equation:
PV*(1 + i)^n + PMT*(1 + iX)*[(1+i)^n - 1]/i + FV = 0
Where: X = 0 for end of period payments, and
X = 1 for beginning of period payments
From this equation, functions which solve for the individual variables can be derived. For a detailed explanation of the derivation of this equation, see the comments in the file src/calculation/fin.c from the GnuCash source code. The A, B, and C variables are defined first, to make the later equations simpler to read.
A = (1 + i)^n - 1
B = (1 + iX)/i
C = PMT*B
n = ln[(C - FV)/(C + PV)]/ln((1 + i)
PV = -[FV + A*C]/(A + 1)
PMT = -[FV + PV*(A + 1)]/[A*B]
FV = -[PV + A*(PV + C)]
The solution for interest is broken into two cases.
The simple case for when PMT == 0 gives the solution:
i = [FV/PV]^(1/n) - 1
The case where PMT != 0 is fairly complex and will not be presented here. Rather than involving an exactly solvable function, determining the interest rate when PMT !=0 involves an iterative process. Please see the src/calculation/fin.c source file for a detailed explanation.
Example: Monthly Payments¶
Let’s recalculate Example: Monthly Payments, this time using the mathematical formulas rather than the Loan Repayment Calculator. What is your monthly payment on a $100000 30 year loan at a fixed rate of 4% compounded monthly?
First, let’s define the variables: n = (30*12) = 360, PV = 100000, PMT = unknown, FV = 0, i = 4%=4/100=0.04, CF = PF = 12, X = 0 (end of payment periods).
The second step is to convert the nominal interest rate (i) to the effective interest rate (ieff). Since the interest rate is compounded monthly, it is discrete, and we use: ieff = (1 + i/CF)^(CF/PF) - 1, which gives ieff = (1 + 0.04/12)^(12/12) - 1, thus ieff = 1/300 = 0.0033333.
Now we can calculate A and B. A = (1 + i)^n - 1 = (1 + 1/300)^360 - 1 = 2.313498. B = (1 + iX)/i = (1 + (1/300)*0)/(1/300) = 300.
With A and B, we can calculate PMT. PMT = -[FV + PV*(A + 1)]/[A*B] = -[0 + 100000*(2.313498 + 1)] / [2.313498 * 300] = -331349.8 / 694.0494 = -477.415296 = -477.42.
Answer: You must make monthly payments of 477.42.
House Mortgage (How-To)¶
A house mortgage can be setup using the account structure present in Setting Up Accounts.
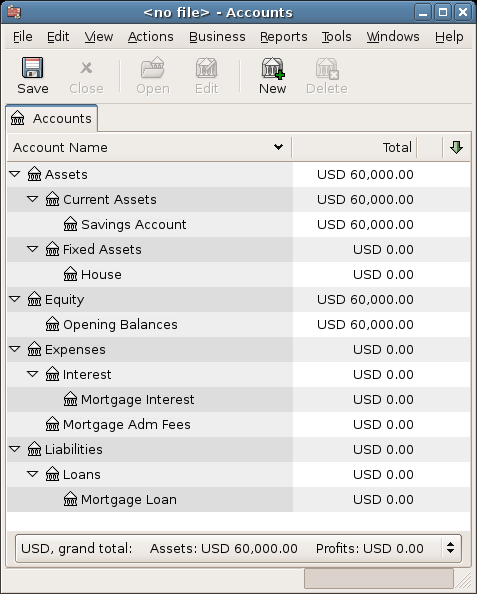
As an example, assume you have $60k in you bank account, and you buy a $150k house. The mortgage is charging 6% APR, and has administrative fees (closing costs, etc) of 3%. You decide to put $50k down, and thus will need to borrow $103k, which will give you $100 after the closing costs are paid (3% of $100k).
Your accounts before borrowing the money:
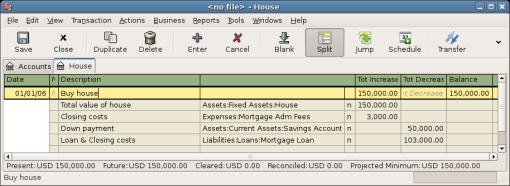
The purchase of the house is recorded with a split transaction in the Assets:House account, with $50k coming from the bank (IE: your down payment), and $100k coming from the Mortgage. You can place the $3k closing costs in the same split, and we increase the house loan to $103k to include the closing costs as well.
Account |
Increase |
Decrease |
Assets:Fixed Assets:House |
$150,000 |
|
Assets:Current Assets:Bank |
$50,000 |
|
Liabilities:Loans:Mortgage Loan |
$103,000 |
|
Expenses:Mortgage Adm Fees |
$3000 |
The split will look like this in the Assets:Fixed Assets:House Account:
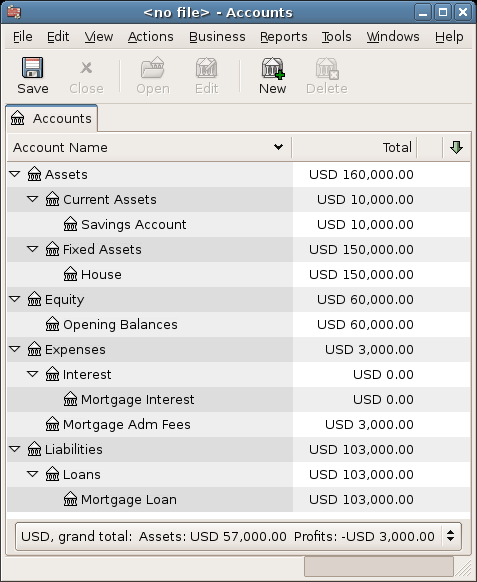
Which will give a Chart of Accounts like this:
A Personal Loan to a friend (How-To)¶
It is not always you are borrowing money from the bank, sometimes you borrow money from your family, or perhaps even lend money to a friend. This How-To chapter will describe one way to handle lending money to a friend.
We are basing this How-To on the following generic account structure.
-Asset
-Bank
-Bank Account
-Money owed to you
-Person
-Income
-Interest Income
-Person
This example will show how to track a personal loan of 2,000 USD (default currency) to your friend Peter
Loan Specifications¶
Peter wants to borrow $2,000 dollars from you and plans to pay you back monthly for the next 18 months. Since he is your friend, (but not that close) you both agree on a yearly interest rate of 5%.
In summary we have the below details. Peter’s loan details:
Pinciple Amount - $2,000
Term - 18 months with 12 payments per year
Annual Percentage Rate: 5%
Monthly Payment : ??
So how do you calculate the Monthly Payment?
You have a number of different options, like paper and pen, Linux Calculator, Open Office’s Calc module, but the easiest is to use GnuCash Loan Repayment Calculator. This tells you that the Monthly Payment should be $115.56.
But you need to know how much of this is Interest and how much is Principal to be able to do a proper bookkeeping. For this you need a more powerful tool, something like the Calc module in OpenOffice.org, and in particular the PMT function.

Accounts for the loan¶
Let’s start with the following accounts (all accounts have the same currency, in this case USD)
Assets:Bank:USD
Assets:Money owed to you:Peter
Income:Interest Income:Peter
Equity:Opening Balances:USD
Lending the money¶
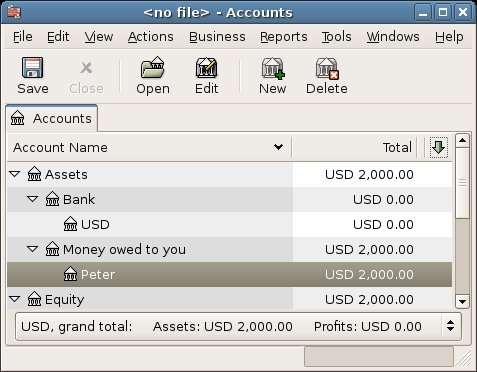
When you have lent money to your friend, you have in fact moved money from an Asset account (like Bank, Checking or similar) to your Asset account Money owed to you. To record this you enter the following transaction into the Assets:Money owed to you:Friend account.
Account |
Increase |
Decrease |
Assets:Money owed to you:Friend |
$2,000 |
|
Assets:Bank:USD |
$2,000 |
Receiving first payment¶
When the first payment ($115.56) is received, you will need to determine how much is for the principal loan, and how much is for the loan interest.
Outstanding loan amount this period = $2,000
Payment per month = $115.56
Payment breakdown
5%/12 * $2,000 = $8.33 Interest
$115.56 - $8.33 = $107.23 Principal
This can be translated to the following GnuCash entry

The balance on Peter’s loan is now $2,000 - $107.23 = $1,892.77
Receiving second payment¶
When the second payment ($115.56) is received, you will again need to determine how much is for the principal loan, and how much is for the loan interest.
Outstanding loan amount this period = $1,892.77
Payment per month = $115.56
Payment breakdown
5%/12 * $1,892.77 = $7.89 Interest
$115.56 - $7.89 = $107.67 Principal
This can be translated to the following GnuCash entry
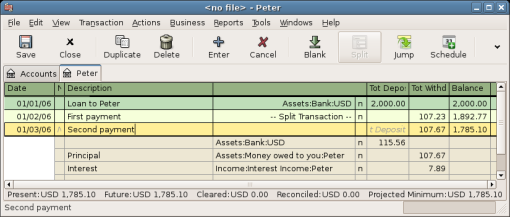
The balance on Peter’s loan is now $1,892.77 - $107.67 = $1,785.10
The Chart of accounts looks now like this
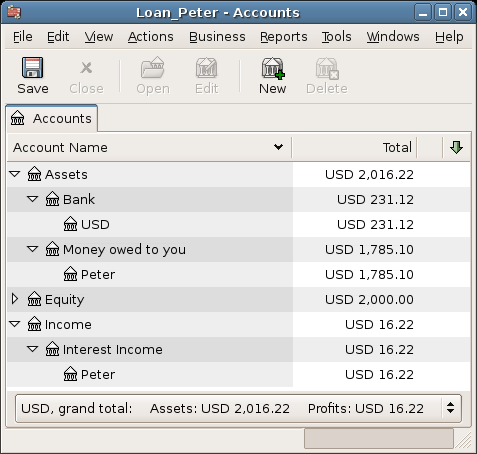
As you can see, the interest varies for every month, as well as the principal amount. So for every payment you receive you need to calculate the proper amounts for your various split entries.
The interest amount will be less and less for every payment (since it is calculated on a smaller loan amount all the time), until the last payment where it is more or less 0. Please review the Figure of Detailed view over private loan to Peter for more details
Automobile Loan (How-To)¶
The Automobile Loan, or in common terms, Car Loan, is treated more or less exactly as the House loan. The only difference is different accounts, and different interest rates.
Basic Car Loan Account Structure -Asset -Current Assets -Savings Account -Fixed Assets -Car -Liability -Loans -Car Loan -Expenses -Interest -Car Loan Interest -Car Loan Adm Fees
For more information, please check House Mortgage (How-To)
Reconciling with the Loan Statements (How-To)¶
Reconciling a loan statement is no different from reconciling a bank or credit card statement.
During the period you should have recorded all the various loan related transactions, and every one of them are touching the Liability:Loans:Loan account. For instance, paying off a bit of the loan decreases your Bank Account, and increases the Loan account, Loan Interest as well as perhaps Loan administration fee.
With the loan statement in your hands, open the Loan account, start the reconcile assistant, and tick of all the various transaction you have recorded. When you have finished, the reconciling difference should be 0, and if it is not, then you will have to go through the account and compare it with the loan statement to find the difference. When you have reached a 0 in difference, then your loan account is reconciled and you can finish the Reconcile assistant.
For more information on how to Reconcile, please check Reconciliation
Selling a house or a car (How-To)¶
When you will record the selling of your house in GnuCash you have some different options. Here we will go through two of them, one in which you only recorded the purchase amount, and now the selling amount. The other where you have followed the ups and downs on the property market and registered various Unrealized gains over the time.
Simple Transaction¶
In this way you only record the proper sale amount.
Let’s work through two samples of selling a house, one with a profit, and one with a loss. If you want to sell a car instead, just substitute the house account with a car account.
-Assets -Fixed Assets -House -Current Assets -Saving -Income -Capital Gains Long -House
You bought a house for $300,000 once upon a time, and now managed to sell it for $600,000. How do you record this?
To record this you need to increase our bank account with the $600k, and decrease some other accounts with $600k. The house account only contains $300k which is what you bought it for, so you move this amount to your bank account. That means you are lacking $300k. This amount you fetch from the Income:Captial Gains Long:House account. The split transaction you enter into your bank account (Assets:Current Assets:Saving) should look like this.
Selling an asset (house) with a profit¶ Account
Increase
Decrease
Assets:Current Assets:Saving
$600,000
Assets:Fixed Assets:House
$300,000
Income:Capital Gains Long:House
$300,000
You bought a house for $300,000 once upon a time, but due to a newly created airport, could only sell it for $230,000. How do you record this?
To record this you need to increase your bank account with the $230k, and decrease some other accounts with $230k. The house account contains $300k which is more than what you sold it for. So let’s move $230k of it to your bank account. After this you have $70k remaining in your house account which needs to be removed. You move it to our Income:Capital Gains Long:House account, which will indicate a loss. The split transaction you enter into your house account (Assets:Fixed Assets:House) should look like this.
Selling an asset (house) with a loss¶ Account
Increase
Decrease
Assets:Fixed Assets:House
$300,000
Assets:Current Assets:Saving
$230,000
Income:Capital Gains Long:House
$70,000
A More Complex Transaction¶
In this example, we will touch a little on some more complicated accounting principles. For more details on this subject, please check Capital Gains
Here we will only touch on the case when you have accurately estimated the current value of your house. For the other cases (over-, and under-estimated), please check Capital Gains.
-Assets -Fixed Assets -House -Cost -Unrealized Gain -Current Assets -Saving -Income -Realized Gain -House -Unrealized Gain -House
You bought a house for $300,000 once upon a time, and over the years kept a close look on the market and updated your records with the estimated current value of your house. At the time you want to sell it, you have determined that the current market value is $600,000.
The difference between $600,000 (estimated market value) and $300,000 (purchase value) is the current Unrealized Gain value. Therefore you have a total of $300,000 in your Assets:Fixed Assets:House:Unrealized Gain account
How do you record this sell transaction?
To record this you need to increase your bank account with the $600k, and decrease some other accounts with $600k. You must first change from unrealized gain to realized gain for your Income accounts. Lastly you need to transfer the full amounts from the Assets:Fixed Assets:House sub-accounts.
The transaction you enter into your Income:Realized Gain:House account account should look like this.
Account |
Increase |
Decrease |
Income:Realized Gain:House |
$300,000 |
|
Income:Unrealized Gain:House |
$300,000 |
The transaction you enter into your Assets:Current Assets:Saving account should look like this.
Account |
Increase |
Decrease |
Assets:Current Assets:Saving |
$600,000 |
|
Assets:Fixed Assets:House:Cost |
$300,000 |
|
Assets:Fixed Assets:House:Unrealized Gain |
$300,000 |
After having recorded these transactions you see that your House Asset have a value of 0, your Savings account have increased with $600,000, and lastly, the Income:Realized Gain have increased to $300,000.